[bibshow file=library.bib key_format=cite]
[wpcol_1half id="" class="" style=""]
Spike Timing Dependent Plasticity
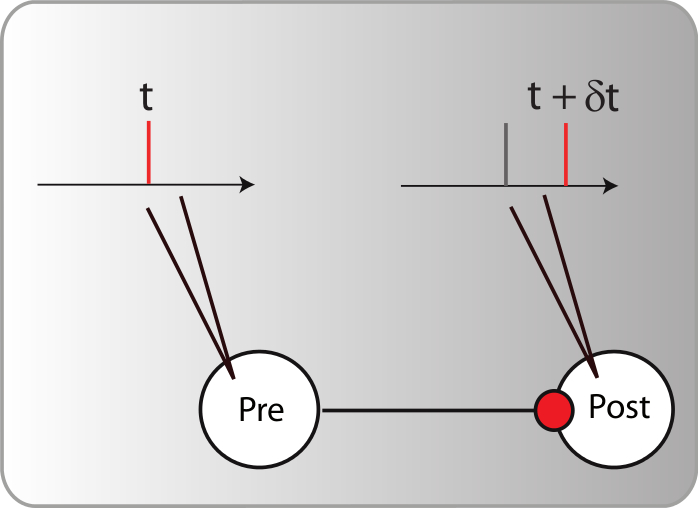
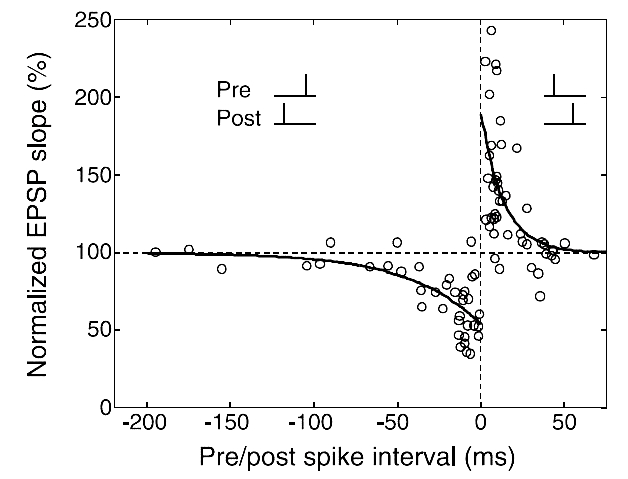
The best experimental setup for exploring plasticity in a controlled manner is the in vitro setup. By using pairs of neurons clearly isolated and connected (using either brain slices or cultured neurons), one can patch the pre- and the post-synaptic neuron and observe the synaptic modifications between them according to their discharge. Based on those controlled experiments, the most recent and promising candidate to support unsupervised learning algorithms in the brain, based on neuronal activity, is the spike timing dependent plasticity (STDP). There is indeed several evidence [bibcite key=Bi1998,Markram1997,Gerstner1996] in neocortex that the efficiency of a synaptic connection between two neurons may be regulated by the precise timing of the joint activity of the neurons. This postulate, originally made by [bibcite key=Hebb1949] , has been demonstrated in a lot of in vitro experimental studies in the form of the STDP rule. This is an associative rule that needs to be distinguished from short term plasticity or homeostasis phenomena, involving only integration of pre-synaptic activity [bibcite key=Tsodyks2000,Turrigiano2004]. As one can see in Figure, taken from [bibcite key=Bi1998], when pre-post pairings are made repeatedly at a fixed frequency of 1 Hz, with a particular time difference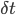 
between pre and post spikes, synaptic modifications are observed whose magnitude depends on 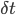. For positive values of 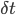, when pre-synaptic spike occurs before the post, the synapse is potentiated. Oppositely, if 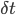is negative, the synapse is depressed. Both mechanisms occur in relatively short time windows of 
20 ms, and a double exponential fit made on the data is the classical shape everybody has in mind when talking about STDP. That 20 ms time scale is the time window for triggering a change, but the actual change happens much more slowly.
While some recent evidence may suggests that STDP can also be found in vivo [bibcite key=Crochet2006,Zhang1998,Young2007a,Jacob2007], the impact of such a rule on a network level is still misunderstood, and part of the problem comes from the fact that there is a lack of data on the properties and the relevance of STDP in vivo. The STDP phenomenon as seen in vitro is appealing from a theoretical point of view. If a pre-synaptic spike occurs just before a post-synaptic one, the strength of the synapse between the two neurons tends to be increased. Conversely, if the pre-synaptic spike comes just after a post-synaptic one, the synaptic strength tends to be decreased. This rule establishes a link with Hebb's postulate and could allow neurons to learn causal chains of information: if pre-synaptic information is important in the discharge of the post-synaptic neuron, then synapse is strengthened, otherwise it is weakened. Interestingly, rules symmetric in sign have been observed in the electro senseory lobe of the electric fish by [bibcite key=Bell1997] and have been used in models to decorrelate the sensory stream from expected inputs linked with the motor-induced reafference.
[/wpcol_1half]
[wpcol_1half_end id="" class="" style=""]
[/wpcol_1half_end]
[wpcol_1half id="" class="" style=""]
[/wpcol_1half]
[wpcol_1half_end id="" class="" style=""]
STDP as an optimization principle
Since this seminal work, several theories have been proposed for a conceptual explanation of these STDP curves. The promising link between STDP and the Hebbian rule has led several authors to try to find a more generic optimization principle behind this canonical shape. The quest is "can STDP be seen as a biological response to an optimization problem?" with a goal function like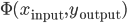 
, if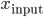 
are the inputs to the neuron, and 
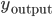its responses. Are the shapes of those curves telling us something about the learning strategies performed by the neuron? According to [bibcite key=Toyoizumi2007,Chechik2003], STDP could be seen as an attempt, by the neurons, to maximize the transmission of information and therefore the mutual information between inputs and outputs, 
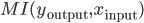. For [bibcite key=Bohte2005b], STDP is more a way to reduce the variability of the output knowing the input: 
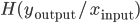(with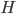 
being the entropy). We can cite other examples such as slow feature analysis [bibcite key=Sprekeler2006], where STDP aims to decompose the signals into a basis of signals, slowly varying in time, or the predictive coding [bibcite key=Rao2001] theory, where STDP is used to encode only time differences. Nevertheless, as we will see later, since STDP is still, from a biological point of view, a phenomenon which is not understood, all these theories, even if conceptually promising, can not pretend to understand STDP in its globality.
[/wpcol_1half_end]
From a modeller's point of view, the rule is ill defined. A good review on all the important aspects of such modelling is given in [bibcite key=Morrison2008]. In its most widely used formulation, one can model STDP with the following system of equations:
\begin{equation}
\delta w = \lambda \left\{
\begin{array}{ll}
a_{\mathrm{pot}} w^{\mu_{\mathrm{pot}}}e^{-\frac{\delta t}{\tau_{\mathrm{pot}}}} & \textrm{if }
\delta t=t_{\mathrm{post}}-t_{\mathrm{pre}} > 0 \\
a_{\mathrm{dep}} w^{\mu_{\mathrm{dep}}}e^{-\frac{\delta t}{\tau_{\mathrm{dep}}}} & \textrm{if }
\delta t=t_{\mathrm{post}}-t_{\mathrm{pre}} < 0 \\
\end{array} \right.
\end{equation}
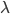is the learning rate, 
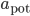and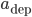 
the scaling increments of the synaptic weights performed at each pairing, for potentiation and depression. Each time a pre or a post-synaptic event appears, weights are updated accordingly. 
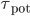and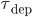 
are the time constants of the double exponential shape observed in biological data, such as the one that can be seen in Figure. Typical values are in the range 10-30 ms. 
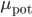and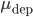 
are generic exponents to model the fact that weight increments can depend on the current values of the weights.
Taking advantage of the exponential, the most efficient way to implement this systems, at the synapse level, is to define two local variables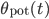 
and 
, such that:
\begin{equation}
\begin{array}{l}
\frac{d\theta_{\mathrm{pot}}(t)}{dt} = -\frac{\theta_{\mathrm{pot}}(t)}{\tau_{\mathrm{pot}}} \\
\frac{d\theta_{\mathrm{dep}}(t)}{dt} = -\frac{\theta_{\mathrm{dep}}(t)}{\tau_{\mathrm{dep}}}
\end{array}
\label{stdp_eq}
\end{equation}
Each time a pre-synaptic spike occurs,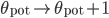 
, and each time a post synaptic spike occurs, 
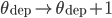. In this case, if 
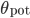and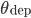 
are not bounded, the integration scheme of the STDP is said to be all-to-all. All previous pre- or post-synaptic spikes contribute to the modification of the weight at time 
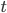, since they have an impact on 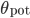and .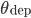
In the so-called nearest-neighbour interaction scheme, 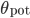and 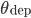are bounded by 1, and only the nearest either pre or post synaptic spike is considered for potentiation or depression. This difference is important, because STDP in its basic form with an all-to-all interaction scheme is not compatible with the BCM theory, as shown in [bibcite key=Izhikevich2003]. Only the nearest-neighbour scheme can provide a BCM behaviour with the rule. The values of 
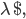a_{\mathrm{pot}}$, 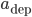, , 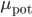, 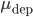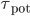and 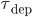are selected according to the STDP desired rule. To simplify the following notations, we set 
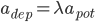(and thus we should have 
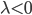, because depression decreases the weight). The pairing scheme used during all the the simulations is all-to-all, meaning that all the interactions between pre and post synaptic spikes are taken into account.
[wpcol_1half id="" class="" style=""]
[/wpcol_1half]
[wpcol_1half _end id="" class="" style=""]
Weight-dependence of STDP
Regarding the weight modifications performed by such plasticity rules, there are two main classes of STDP rules that are commonly used in modelling studies of neuronal networks. They are categorized as either "additive" or "weight-dependent", depending on how current synaptic weight impacts the change in the weight of the synapse [bibcite key=Guetig2003]. These classes are established with the exponents 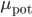and 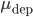. If both are set to 0, then the STDP is "additive". Each time a weight modification is made, increments are only determined by 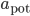and 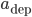, without taking into account the current weight of the synapse. The rule needs a hard bound thresholding to constrain the weights between [
,
].
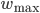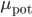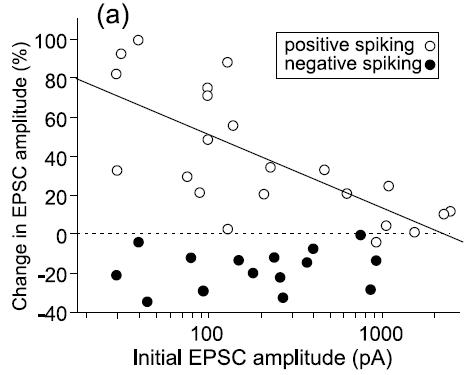
Oppositely, in the weight-dependent rule, the weight increments are a function of the current weight of the synapse. This is the case if and 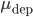are positive. The biological evidence for ``additive''-only rules is quite thin. The original data for STDP, and especially the synaptic modification observed as a function of the initial amplitude of the EPSP show (see Figure) that the relative changes are not similar for potentiation and depression. Modifications for potentiation seem to be independent of the initial amplitude of the EPSP, while this is not the case for depression. \cite{Bi1998} proposed, initially, a log-linear relationship for depression, while potentiation is much more additive. 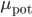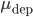For a precise fit, see [bibcite key=Morrison2008,Standage2007], but the exact values for and are not crucial, as long as they are not zero. As pointed out in [bibcite key=Guetig2003], the additive case, often used in models, is a very particular case with particular dynamics. It has been shown in [bibcite key=Rossum2000,Billings2009], through a Fokker Plank approach, that an additive STDP rule always drive the weight distribution to a bimodal one, with all weights being clipped eithe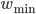r at or at 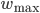. Nevertheless, they encourage synaptic competition and allow a better storage of patterns [bibcite key=Fusi2007]. As we will see in the following, they are less sensitive to the memory retention problem occurring in recurrent networks. Moreover, it is also known that in cortex, and also in the cerebellum a lot of the synapses are considered as almost silent. One could see here the evidence for bimodal distribution resulting from the additive rules. On the contrary, weight-dependent rule leads to a unimodal distribution of the weights, more biologically plausible, but does not allow the emergence and the survival of neuronal structures in balanced random networks [bibcite key=Billings2009,Morrison2007].
STDP at inhibitory synapses
Although inhibitory interneurons modulate many neuronal processes, the evidence for plasticity at inhibitory synapses remains scarce. Some studies report strengthening of inhibitory synapses in negative rate covariance regimes [bibcite key=Komatsu1993], and spike timing dependent plasticity of inhibitory synapses has also been reported [bibcite key=Haas2006] as well as spike timing dependent depression of excitatory synapses on fast spiking inhibitory interneurons. Almost all models of plastic networks consider that only excitatory synapses are plastic, because most of the biological evidence for STDP has been gathered for synapse between excitatory neurons, far more numerous and easy to patch than inhibitory ones. Nevertheless, the question of plasticity at inhibitory synapses remains open, and could greatly help stabilization in recurrent networks. [bibcite key=Haas2006] found an anti-Hebbian rule for inhibitory synapses. Pre-post pairing led to reinforcement of the synapse, meaning to an increase in the amplitude of the post-synaptic inhibitory post synaptic potential (IPSP), while post-pre led to a decrease. This anti-Hebbian rule, from a conceptual point of view, offers nice theoretical possibilities. In artificial neural networks, anti-Hebbian rules for inhibition are important to balance the changes at the excitatory synapses and allow the network to perform robust principal or independent component analysis [bibcite key=Plumbley1993].